nLab vector meson dominance
Context
Fields and quanta
fields and particles in particle physics
and in the standard model of particle physics:
matter field fermions (spinors, Dirac fields)
| flavors of fundamental fermions in the standard model of particle physics: | |||
|---|---|---|---|
| generation of fermions | 1st generation | 2nd generation | 3d generation |
| quarks () | |||
| up-type | up quark () | charm quark () | top quark () |
| down-type | down quark () | strange quark () | bottom quark () |
| leptons | |||
| charged | electron | muon | tauon |
| neutral | electron neutrino | muon neutrino | tau neutrino |
| bound states: | |||
| mesons | light mesons: pion () ρ-meson () ω-meson () f1-meson a1-meson | strange-mesons: ϕ-meson (), kaon, K*-meson (, ) eta-meson () charmed heavy mesons: D-meson (, , ) J/ψ-meson () | bottom heavy mesons: B-meson () ϒ-meson () |
| baryons | nucleons: proton neutron |
(also: antiparticles)
hadrons (bound states of the above quarks)
minimally extended supersymmetric standard model
bosinos:
dark matter candidates
Exotica
Quantum Field Theory
algebraic quantum field theory (perturbative, on curved spacetimes, homotopical)
Concepts
quantum mechanical system, quantum probability
interacting field quantization
Theorems
States and observables
Operator algebra
Local QFT
Perturbative QFT
Contents
Idea
The phenomenon or principle called vector meson dominance (VMD) is a tight relation between quantum hadrodynamics and quantum electrodynamics, where the electrically neutral light vector meson fields (the neutral rho-meson , the omega-meson and the phi-meson) are seen to be on par with, or even identified with, the electromagnetic hadronic current , at least to some approximation.
Phenomenology
In particle physics phenomenology, vector meson dominance is the observation that the interaction of hadrons with photons is dominated by interactions that procceed via excange of vector mesons.
Specifically, the decay of electron/positron-pairs into hadrons
(reverse to the purely leptonic decay of hadrons) is dominated by the light vector mesons, in that the scattering cross section is peaked at those energies corresponding to the rest masses of the vector mesons:
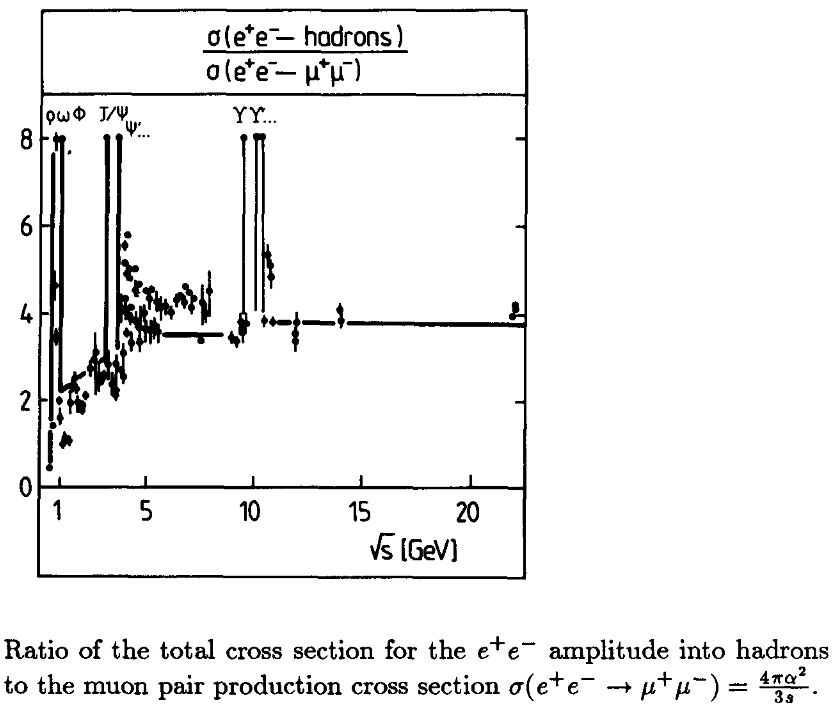
The first graphics shows the measured cross section (in units of that of the decay of electron dileptons into muon dileptons): The light vector mesons ρ, ω and ϕ correspond to the the spikes below 1 GeV, the further spikes correspond to heavy vector mesons, with charmonium around 4 GeV.
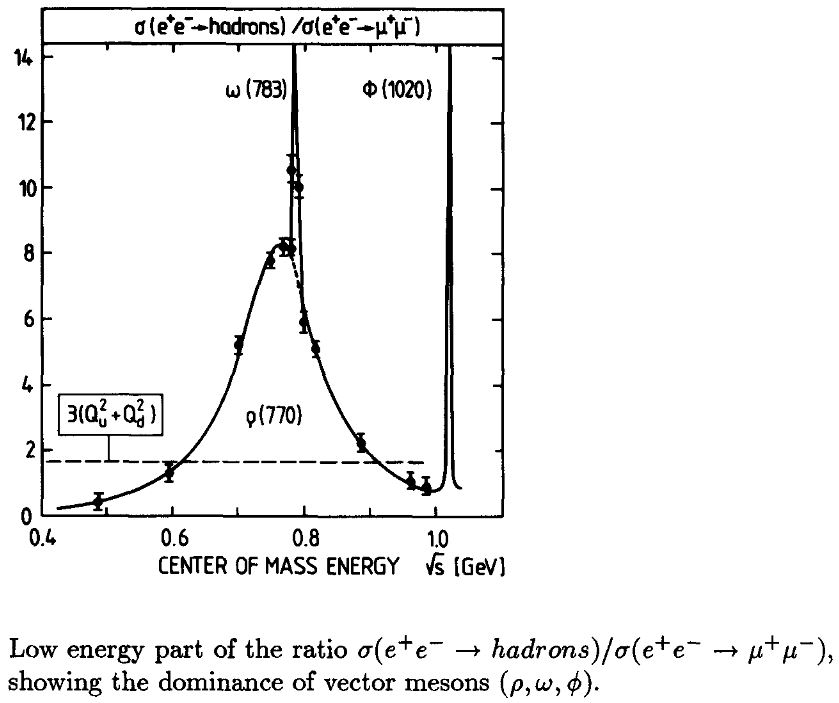
The second graphics shows the same data, now zoomed into the region of the light vector mesons. One sees clearly that in this region the graph of the scattering cross section is completely dominated first of all by the broad ρ peak at a mass of MeV (see also Murphy-Yount 71, Fig. 4), accompanied just by two sharp spikes, corresponding to the ω at MeV and the ϕ at MeV (see also Schildknecht 72, Table 1).
Theory
In the effective field theory of quantum hadrodynamics, vector meson dominance refers to a proposal for how to formulate the theory guided by the above phenomenology:
Here the dominance is encoded by the field-current identity (Gell-Mann & Zachariasen 61, Kroll, Lee & Zumino 76, (1.3), Sakurai 69, p. 54 onwards, review in Piller-Weise 90, (4)):
essentially identifying the electromagnetic hadron current with the joint neutral light vector meson field.
This implies in particular that all coupling constants of interactions with an omega-meson/neutral rho-meson are proportional, by the same factor, to the corresponding electromagnetic coupling (reviewed in Schildknecht 05, p. 3).
In terms of a Lagrangian density, this is encoded by meson/photon mixed terms of the following form (Kroll, Lee & Zumino 76, (2.7),Sakurai 69, p. 67):
obtained from the Lagrangian density of Maxwell theory by exchanging a photon field variable with a vector meson field (reviewed in OCPTW 95, p. 10, Schildknecht 05, p. 4).
There is also an alternative, supposedly equivalent, Lagrangian formulation, less elegant but now in more widespread use. To distinguish the two one speaks of “VMD1” for the formulation (1) and of “VMD2” for the alternative formulation (reviewed in OCPTW 95. (26), Schildknecht 05, (8)).
Properties
Derivation from holography
From OCPTW 95:
No direct translation between the Standard Model and VMD has yet been made.
From Rho et al. 16:
One can make chiral perturbation theory consistent with QCD by suitably matching the correlators of the effective theory to those of QCD at a scale near . Clearly this procedure is not limited to only one set of vector mesons; in fact, one can readily generalize it to an infinite number of hidden gauge fields in an effective Lagrangian. In so doing, it turns out that a fifth dimension is “deconstructed” in a (4+1)-dimensional (or 5D) Yang–Mills type form. We will see in Part III that such a structure arises, top-down, in string theory.
this holographic QCD model comes out to describe — unexpectedly well — low-energy properties of both mesons and baryons, in particular those properties reliably described in quenched lattice QCD simulations.
One of the most noticeable results of this holographic model is the first derivation of vector dominance (VD) that holds both for mesons and for baryons. It has been somewhat of an oddity and a puzzle that Sakurai's vector dominance — with the lowest vector mesons ρ and ω — which held very well for pionic form factors at low momentum transfers famously failed for nucleon form factors. In this holographic model, the VD comes out automatically for both the pion and the nucleon provided that the infinite KK-tower is included. While the VD for the pion with the infinite tower is not surprising given the successful Sakurai VD, that the VD holds also for the nucleons is highly nontrivial. It turns out to be a consequence of a holographic Cheshire Cat phenomenon
Related concepts
effective field theories of nuclear physics, hence for confined-phase quantum chromodynamics:
References
General
The original articles:
-
Murray Gell-Mann, Fredrik Zachariasen, Form Factors and Vector Mesons, Phys. Rev. 124, 953 (1961) (doi:10.1103/PhysRev.124.953)
-
Norman M. Kroll, T. D. Lee, Bruno Zumino, Neutral Vector Mesons and the Hadronic Electromagnetic Current, Phys. Rev. 157, 1376 (1967) (arXiv:10.1103/PhysRev.157.1376)
-
Jun John Sakurai, Chapter III of: Currents and Mesons, Chicago Lectures in Physics, based on notes by George Barry, University of Chicago Press (1969) (ISBN: 9780226733838)
Review:
-
Fred V. Murphy, David E. Yount, Photons as hadrons, Sci.Am. 225N1 (1971) 1, 94-104 (spire:41546, doi:10.1038/scientificamerican0771-94)
-
Dieter Schildknecht, Vector meson dominance, photo- and electroproduction from nucleons, in: Photon-Hadron Interactions II Springer Tracts in Modern Physics, vol 63. Springer 1972 (doi:10.1007/BFb0041507)
-
G. Piller, Wolfram Weise, Vector meson dominance: Selected topics 1990 (spire310958, pdf)
-
H. B. O’Connell, B. C. Pearce, A. W. Thomas, A. G. Williams, Rho-omega mixing, vector meson dominance and the pion form-factor, Prog. Part. Nucl. Phys. 39:201-252, 1997 (arXiv:hep-ph/9501251)
-
Dieter Schildknecht, Vector Meson Dominance, Acta Phys. Polon. B37:595-608, 2006 (arXiv:hep-ph/0511090)
See also
- Wikipedia, Vector meson dominance
More:
-
H. B. O’Connell, A. G. Williams, M. Bracco, G. Krein, Vector Meson Mixing and Charge Symmetry Violation, Phys. Lett. B370:12-16, 1996 (arXiv:hep-ph/9510425)
-
A. G. Williams, New results in vector meson dominance and rho meson physics, Proceedings of the APCTP Workshop on Astro-Hadron Physics, “Properties of Hadrons in Matter”, Seoul, 25-31 October, 1997 (arXiv:hep-ph/9712405)
-
M. Benayoun, P. David, L. DelBuono, O. Leitner, A Global Treatment Of VMD Physics Up To The : I. Annihilations, Anomalies And Vector Meson Partial Widths, Eur. Phys. J. C65:211-245, 2010 (arXiv:0907.4047)
-
M. Benayoun, P. David, L. DelBuono, O. Leitner, A Global Treatment Of VMD Physics Up To The : II. Decay and Hadronic Contributions To , Eur. Phys. J. C68:355-379, 2010 (arXiv:0907.5603)
-
Avner Karasik, Vector dominance, one flavored baryons, and QCD domain walls from the “hidden” Wess-Zumino term (arXiv:2010.10544)
Via holographic QCD
Derivation of vector meson dominance via holographic QCD:
-
D.T. Son, M.A. Stephanov, QCD and dimensional deconstruction, Phys. Rev. D69 (2004) 065020 (arXiv:hep-ph/0304182)
(from the point of view of hidden local symmetry)
-
Sungho Hong, Sukjin Yoon, Matthew Strassler, On the Couplings of Vector Mesons in AdS/QCD, JHEP 0604 (2006) 003 (arXiv:hep-th/0409118)
-
Sungho Hong, Sukjin Yoon, Matthew Strassler, On the Couplings of the Rho Meson in AdS/QCD (cds:816440, arXiv:hep-ph/0501197)
-
Leandro Da Rold, Alex Pomarol, Chiral symmetry breaking from five dimensional spaces, Nucl. Phys. B721:79-97, 2005 (arXiv:hep-ph/0501218)
and specifically in the Witten-Sakai-Sugimoto model:
- Tadakatsu Sakai, Shigeki Sugimoto, p. 18 and Section 5 of: More on a holographic dual of QCD, Progr. Theor. Phys. 114: 1083-1118, 2005 (arXiv:hep-th/0507073)
Last revised on October 22, 2020 at 06:53:58. See the history of this page for a list of all contributions to it.